El contenido de esta entrada es demasiado técnico, pero para entender lo que es un monopolo sobre masa, que era el tipo de antena usado en la estación radioeléctrica Consol, es necesario conocer lo que es una antena dipolo. Este apartado puede ser saltado a efectos de conocer el sistema Consol, pero me ha parecido que si quiero exponer el tema con algo de profundidad, me veo obligado a hacerlo así. Ante el primer síntoma de pesadez en la lectura de lo que sigue, el lector tiene su plena libertad para saltárselo o para navegar por otras páginas, reconozco que es demasiado específico y condensado, pero también entiendo que si alguien llega a esta entrada mediante un buscador, ello será debido a que tiene interés en lo que aquí se describe, por lo que al final he optado por incluírlo, dado que es una pieza más dentro de la comprensión del entredicho sistema de posicionamiento. Así pues, pido disculpas anticipadas a las personas que opinen que esto sobra o que está escrito de forma inapropiada, y me decanto al final por mantenerlo. Simplemente, al que le interese, que lo lea, quien por el contrario vea que esta entrada está de más, puede pasar a leer otras entradas o simplemente teclear otra URL y navegar por otra web. Para gustos hay colores, en torno a la pluralidad gira esta página, o procuro eso al menos, y además entiendo perfectamente a los que se lo salten, porque yo ya soy el primero que lee libros de divulgación o libros técnicos saltándome algún que otro párrafo, al menos en la primera lectura, por parecerme inicialmente incomprensible. Quedan las disculpas por escrito.
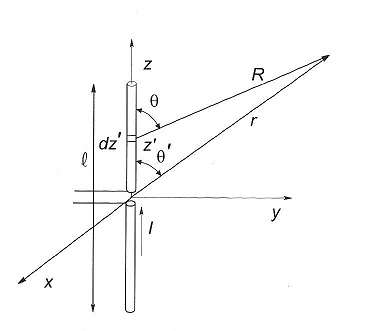
Un dipolo elemental es un elemento de corriente cuya longitud es mucho menor que la longitud de onda, y por el que fluye una corriente uniforme. Aunque podría parecer un caso anómalo, en realidad muchas antenas operando en baja frecuencia tienen un comportamiento similar al mismo, por poseer sus mismas cualidades. Si se supone un hilo de densidad de corriente J = I.delta(x).delta(y) z, siendo la función delta la delta de Dirac, que es una idealización que establece que la densidad de corriente es nula salvo en el origen de coordenadas, y aplicando la ecuación del potencial vector mostrada en la anterior sección, utilizando además las aproximaciones pertinentes, se obtiene, como es lógico, un potencial vector de una única componente según el vector unitario z; pero resulta más práctico representar el resultado en coordenadas esféricas y no cartesianas, y así se obtiene una componente para el potencial vector según el vector unitario theta proporcional al seno de theta y una componente según el vector unitario phi nula. No existe componente según el vector unitario rho, porque en campo lejano esta componente según el mencionado versor unitario del sistema de coordenadas esféricas es aproximadamente nula.
De esta forma el fasor de campo eléctrico radiado, que es –j veces el producto de la pulsación por el potencial vector, también varía con el seno de theta y presenta un factor de fase que equivale a la tardanza en producirse los efectos lejos de la antena (campos) posteriormente a las causas que los originaron (corriente). Por su parte, la intensidad de campo magnético, que se escribe como el inverso de la permeabilidad multiplicado por el rotacional del potencial vector varía como el seno de theta también, pero su única componente tiene como vector unitario al versor phi.
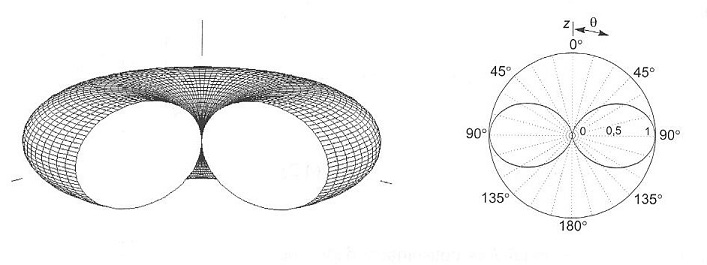
Para calcular el diagrama de radiación de potencia, que es una representación de cómo radia una antena según cada dirección genérica dada por un ángulo theta y un ángulo phi determinados, se obtiene la parte real del producto vectorial del fasor de campo eléctrico y el conjugado del fasor de intensidad del campo magnético, que es el conocido como vector de Poynting y que da cuenta de la potencia que atraviesa la unidad de superficie en el punto genérico bajo análisis, y que como es lógico variará como el cuadrado del seno de theta con otros factores que incluyen el inverso del cuadrado de la distancia y un factor directo constituido por el cuadrado de la longitud del dipolo elemental y el cuadrado del valor eficaz de la corriente. Como desde cualquier punto a una distancia R del dipolo vemos el dipolo de la misma manera, el campo eléctrico y el diagrama de radiación presentan simetría de revolución, y además una forma similar a un toro.
Si ahora calculamos toda la potencia radiada integrando el flujo del vector de Poynting a través de cualquier superficie que encierre el dipolo y dividimos esa potencia radiada por el cuadrado de la corriente a la entrada de la antena se obtiene la resistencia de radiación de la misma, que se puede definir como aquella resistencia que colocada en vez de la antena consumiría por efecto Joule toda la potencia que radia aquélla. Cuanto mayor sea la longitud del dipolo elemental frente a la longitud de onda, mayor será la resistencia de radiación para este caso, y por tanto, más potencia se radiará, y mayor valor poseerá el fasor de campo eléctrico, y por tanto mayor amplitud el campo eléctrico instantáneo.
Todo lo hasta aquí comentado se refiere a campo lejano, es decir, lejos de la posición que ocupa el dipolo elemental. En las inmediaciones del dipolo, los campos que se obtienen se corresponden con los que produciría un dipolo eléctrico con una cierta carga en cada extremo de signos opuestos, y no varían con la frecuencia, esto es, son estáticos. Debido al carácter oscilante de las fuentes, al pasar un medio período de la corriente de excitación, se invierte el sentido de la corriente y los signos de las cargas. Como consecuencia de esto, un dipolo elemental eléctrico se comporta capacitivamente y con una pequeña resistencia de radiación. A una frecuencia de 285 kiloHerzios, un hilo de aproximadamente 100 metros es casi un dipolo elemental, siempre y cuando coloquemos en sus extremos unas superficies conductoras donde pueda almacenarse carga eléctrica. La impedancia de entrada, que es el cociente entre el fasor de tensión y el fasor de corriente a una cierta frecuencia tiene en este caso una componente de tipo capacitivo. Esto es, un dipolo elemental puede verse como un condensador abierto.
De momento me he limitado a presentar una estructura pequeña en relación a la longitud de onda, donde podemos suponer que la distribución de corriente es uniforme. Si las dimensiones de la antena no verifican tal cualidad, habrá interacciones entre todos sus elementos con retardos asociados, de tal forma que ya no se podrá aproximar la corriente por un valor uniforme. Entramos así en el terreno de las antenas dipolo.
El caso más simple de antena dipolo es la antena cilíndrica, consistente en un hilo conductor recto de longitud 2H y radio a muy inferior a la longitud de onda, al que se le alimenta con un generador en el centro. De forma experimental, se ha obtenido que la distribución de corriente para estas clases de antenas es aproximadamente sinusoidal, con valor cero en los extremos, dando así continuidad a lo no conductividad del aire. Para justificar esta distribución de corriente se puede pensar en la antena cilíndrica como una línea de transmisión de líneas paralelas que termina en circuito abierto y que vamos abriendo hasta quedar las dos líneas en posición vertical. Puesto que la línea termina en circuito abierto, aparece una onda estacionaria de corriente, con un nulo en el extremo. Dentro de las antenas dipolo tal vez el caso más común es el del dipolo en lambda/2 o dipolo de media onda, para el valor de H = lambda/4. Para este caso el diagrama de radiación es similar al del dipolo elemental, de forma toroidal, con simetría de revolución, y un haz algo más estrecho.
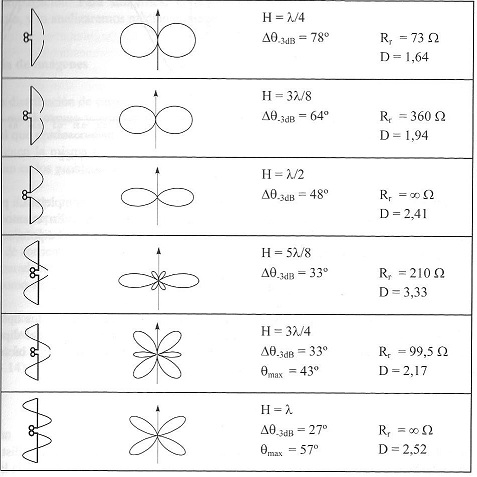
El siguiente esquema representa los parámetros característicos de algunos dipolos de diferentes semilongitudes H, incluyéndose entre estos parámetros a la longitud, el ancho de haz a 3 dB, que representa aquel ángulo que subtiende el diagrama de radiación de potencia con unos valores subtendidos superiores o iguales a la mitad de la densidad de potencia radiada máxima de radiación, así como la resistencia de radiación, y la directividad, la cual es un parámetro que nos da idea del cociente entre el máximo de la densidad de potencia radiada y la densidad de potencia radiada por una antena isotrópica que radiase la misma potencia que la antena bajo análisis. Esto es, la directividad nos viene a informar de lo que concentra la radiación según la dirección de máximo una antena, comparándola con otra que radiando la misma potencia lo hiciese por igual en todas direcciones. Si extendemos este concepto para todas las direcciones tenemos una función de los ángulos theta y phi, conocida como ganancia, que da cuenta de la relación entre la densidad de potencia por metro cuadrado en una dirección frente a la densidad isotrópica de una antena que radiase la misma potencia.
Fuente de las imágenes de esta entrada : Antenas, varios autores, Edicións UPC.
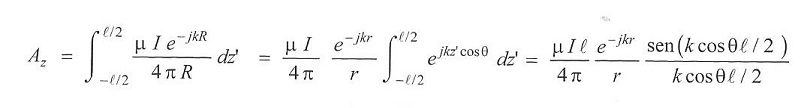
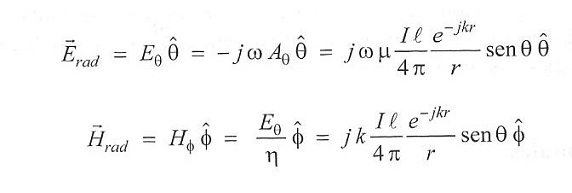
Una entrada muy interesante, la revisare con cuidado. Tu blog parece muy interesante y cuidado, felicitaciones de un estudiante de telecomunicaciones y apasionado de la radiocomunicacion
Muchas gracias. El tema de los radiofaros Consol me resulta apasionante porque tuve la ocasión de estar en las instalaciones por los años 90, cuando todavía se conservaban restos de un transmisor, otras piezas, y las propias antenas.